Shortest Path Visiting All Nodes

You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

 

Example 1:

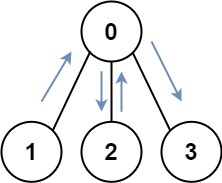
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2:

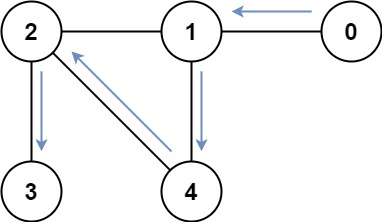
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

 

Constraints:

  • n == graph.length
  • 1 <= n <= 12
  • 0 <= graph[i].length < n
  • graph[i] does not contain i.
  • If graph[a] contains b, then graph[b] contains a.
  • The input graph is always connected.
SOLUTION:
class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)
        if n == 1:
            return 0
        req = (1 << n) - 1
        visited = {}
        queue = []
        for i in range(n):
            queue.append((0 | (1 << i), i))
        lvl = 1
        qi = 0
        while qi < len(queue):
            k = len(queue) - qi
            while k > 0:
                curr, currnode = queue[qi]
                qi += 1
                for u in graph[currnode]:
                    newMask = curr | (1 << u)
                    if newMask == req:
                        return lvl
                    if newMask in visited.get(u, {}):
                        continue
                    visited[u] = visited.get(u, set()).union({newMask})
                    queue.append((newMask, u))
                k -= 1
            lvl += 1
        return -1

Comments

Post a Comment

Popular posts from this blog

Encrypt and Decrypt Strings

You are given a character array keys containing unique characters and a string array values containing strings of length 2. You are also given another string array dictionary that contains all permitted original strings after decryption. You should implement a data structure that can encrypt or decrypt a 0-indexed string. A string is encrypted with the following process: For each character c in the string, we find the index i satisfying keys[i] == c in keys . Replace c with values[i] in the string. Note that in case a character of the string is not present in keys , the encryption process cannot be carried out, and an empty string "" is returned. A string is decrypted with the following process: For each substring s of length 2 occurring at an even index in the string, we find an i such that values[i] == s . If there are multiple valid i , we choose any one of them. This means a string could have multiple possible strings it can decrypt t...
Read more

Degree of an Array

Given a non-empty array of non-negative integers nums , the degree of this array is defined as the maximum frequency of any one of its elements. Your task is to find the smallest possible length of a (contiguous) subarray of nums , that has the same degree as nums .   Example 1: Input: nums = [1,2,2,3,1] Output: 2 Explanation: The input array has a degree of 2 because both elements 1 and 2 appear twice. Of the subarrays that have the same degree: [1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2] The shortest length is 2. So return 2. Example 2: Input: nums = [1,2,2,3,1,4,2] Output: 6 Explanation: The degree is 3 because the element 2 is repeated 3 times. So [2,2,3,1,4,2] is the shortest subarray, therefore returning 6.   Constraints: nums.length will be between 1 and 50,000. nums[i] will be an integer between 0 and 49,999. SOLUTION: from collections import defaultdict class Solution : def findShortestSubArr...
Read more

Minimum Sum of Four Digit Number After Splitting Digits

You are given a positive integer num consisting of exactly four digits. Split num into two new integers new1 and new2 by using the digits found in num . Leading zeros are allowed in new1 and new2 , and all the digits found in num must be used. For example, given num = 2932 , you have the following digits: two 2 's, one 9 and one 3 . Some of the possible pairs [new1, new2] are [22, 93] , [23, 92] , [223, 9] and [2, 329] . Return the minimum possible sum of new1 and new2 .   Example 1: Input: num = 2932 Output: 52 Explanation: Some possible pairs [new1, new2] are [29, 23], [223, 9], etc. The minimum sum can be obtained by the pair [29, 23]: 29 + 23 = 52. Example 2: Input: num = 4009 Output: 13 Explanation: Some possible pairs [new1, new2] are [0, 49], [490, 0], etc. The minimum sum can be obtained by the pair [4, 9]: 4 + 9 = 13.   Constraints: 1000 <= num <= 9999 SOLUTION: class Solution : def minimumSum ( self,...
Read more