Check if Matrix Is X-Matrix

A square matrix is said to be an X-Matrix if both of the following conditions hold:

  1. All the elements in the diagonals of the matrix are non-zero.
  2. All other elements are 0.

Given a 2D integer array grid of size n x n representing a square matrix, return true if grid is an X-Matrix. Otherwise, return false.

 

Example 1:

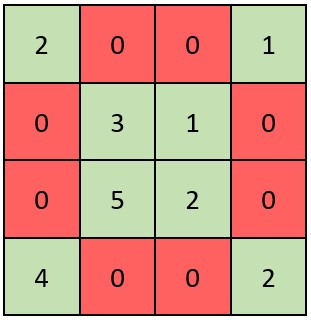
Input: grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
Output: true
Explanation: Refer to the diagram above. 
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.

Example 2:

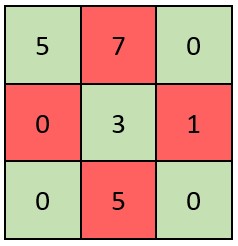
Input: grid = [[5,7,0],[0,3,1],[0,5,0]]
Output: false
Explanation: Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.

 

Constraints:

  • n == grid.length == grid[i].length
  • 3 <= n <= 100
  • 0 <= grid[i][j] <= 105
SOLUTION:
class Solution:
    def checkXMatrix(self, grid: List[List[int]]) -> bool:
        n = len(grid[0])
        for i in range(n):
            for j in range(n):
                if i - j == 0 or i + j == n - 1:
                    if grid[i][j] == 0:
                        return False
                else:
                    if grid[i][j] != 0:
                        return False
        return True

Comments

Post a Comment

Popular posts from this blog

Encrypt and Decrypt Strings

You are given a character array keys containing unique characters and a string array values containing strings of length 2. You are also given another string array dictionary that contains all permitted original strings after decryption. You should implement a data structure that can encrypt or decrypt a 0-indexed string. A string is encrypted with the following process: For each character c in the string, we find the index i satisfying keys[i] == c in keys . Replace c with values[i] in the string. Note that in case a character of the string is not present in keys , the encryption process cannot be carried out, and an empty string "" is returned. A string is decrypted with the following process: For each substring s of length 2 occurring at an even index in the string, we find an i such that values[i] == s . If there are multiple valid i , we choose any one of them. This means a string could have multiple possible strings it can decrypt t...
Read more

Degree of an Array

Given a non-empty array of non-negative integers nums , the degree of this array is defined as the maximum frequency of any one of its elements. Your task is to find the smallest possible length of a (contiguous) subarray of nums , that has the same degree as nums .   Example 1: Input: nums = [1,2,2,3,1] Output: 2 Explanation: The input array has a degree of 2 because both elements 1 and 2 appear twice. Of the subarrays that have the same degree: [1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2] The shortest length is 2. So return 2. Example 2: Input: nums = [1,2,2,3,1,4,2] Output: 6 Explanation: The degree is 3 because the element 2 is repeated 3 times. So [2,2,3,1,4,2] is the shortest subarray, therefore returning 6.   Constraints: nums.length will be between 1 and 50,000. nums[i] will be an integer between 0 and 49,999. SOLUTION: from collections import defaultdict class Solution : def findShortestSubArr...
Read more

Minimum Sum of Four Digit Number After Splitting Digits

You are given a positive integer num consisting of exactly four digits. Split num into two new integers new1 and new2 by using the digits found in num . Leading zeros are allowed in new1 and new2 , and all the digits found in num must be used. For example, given num = 2932 , you have the following digits: two 2 's, one 9 and one 3 . Some of the possible pairs [new1, new2] are [22, 93] , [23, 92] , [223, 9] and [2, 329] . Return the minimum possible sum of new1 and new2 .   Example 1: Input: num = 2932 Output: 52 Explanation: Some possible pairs [new1, new2] are [29, 23], [223, 9], etc. The minimum sum can be obtained by the pair [29, 23]: 29 + 23 = 52. Example 2: Input: num = 4009 Output: 13 Explanation: Some possible pairs [new1, new2] are [0, 49], [490, 0], etc. The minimum sum can be obtained by the pair [4, 9]: 4 + 9 = 13.   Constraints: 1000 <= num <= 9999 SOLUTION: class Solution : def minimumSum ( self,...
Read more